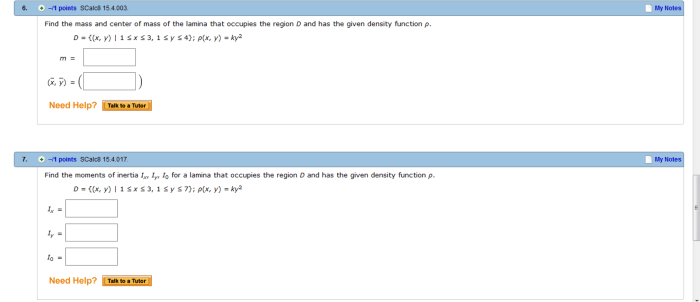
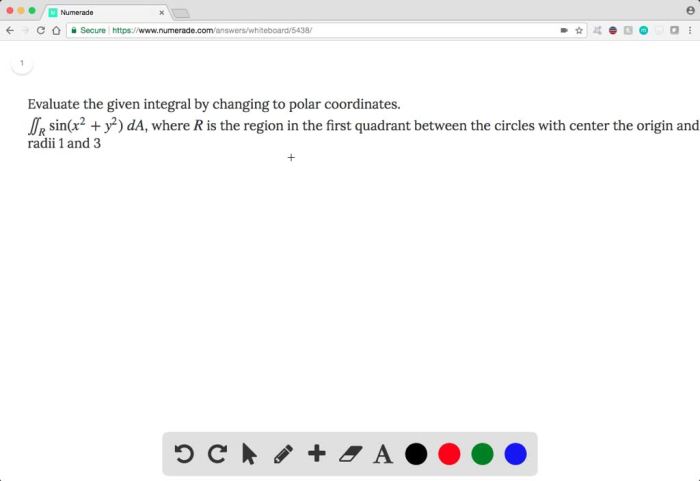
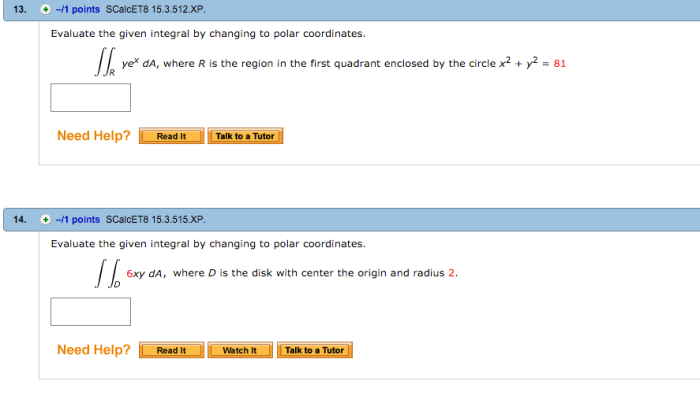
Evaluate the given integral by changing to polar coordinates – Embark on a journey to simplify integral evaluation with the transformative power of polar coordinates. This comprehensive guide unveils the benefits, techniques, and applications of this ingenious approach, empowering you to conquer complex integrals with newfound ease.
Polar coordinates, with their radial distance and angular measure, offer a unique perspective that unlocks new possibilities in integral calculus. Discover the secrets of converting rectangular coordinates to polar coordinates, mastering variable substitution, and defining regions of integration in this polar coordinate paradise.
Integral Evaluation in Polar Coordinates

Integral evaluation in polar coordinates is a powerful technique used to evaluate integrals over regions that are naturally described in terms of polar coordinates. By transforming the integral from rectangular coordinates to polar coordinates, we can often simplify the integration process and obtain solutions that would be difficult or impossible to find using rectangular coordinates.
Conversion and Substitution, Evaluate the given integral by changing to polar coordinates
To convert an integral from rectangular to polar coordinates, we use the following transformations:
- x = r cos(theta)
- y = r sin(theta)
- dA = r dr dtheta
where r is the distance from the origin to the point (x, y) and theta is the angle between the positive x-axis and the line segment connecting the origin to (x, y).
Substituting these transformations into the integral, we obtain:
∫∫ Rf(x, y) dA = ∫∫ Rf(r cos(theta), r sin(theta)) r dr dtheta
Region of Integration
When evaluating integrals in polar coordinates, it is important to carefully define the region of integration. The region is typically described in terms of the limits of integration for r and theta.
- The limits of integration for r specify the range of distances from the origin over which the integral is evaluated.
- The limits of integration for theta specify the range of angles over which the integral is evaluated.
Applications in Calculus
Polar coordinate integration has numerous applications in calculus, including:
- Calculating areas and volumes of regions in the plane and in three-dimensional space.
- Evaluating integrals involving functions that are defined in terms of polar coordinates.
- Solving problems in physics and engineering that involve circular or cylindrical symmetry.
Limitations and Pitfalls
While polar coordinate integration is a powerful technique, it does have some limitations and pitfalls:
- It can only be used to evaluate integrals over regions that are naturally described in terms of polar coordinates.
- It can be difficult to determine the limits of integration for some regions.
- It is important to be aware of the potential for sign errors when converting integrals from rectangular to polar coordinates.
FAQ Resource: Evaluate The Given Integral By Changing To Polar Coordinates
What are the advantages of using polar coordinates for integral evaluation?
Polar coordinates excel in evaluating integrals involving circular or symmetric regions, simplifying complex calculations and yielding elegant solutions.
How do I convert an integral from rectangular to polar coordinates?
To convert an integral, express the integrand in terms of polar variables (r and θ) and apply the appropriate Jacobian determinant.
What are the common applications of polar coordinate integration?
Polar coordinate integration finds widespread use in calculating areas and volumes of circular regions, solving problems in physics (e.g., gravitational force, fluid flow), and analyzing conic sections.